Yx Chart
Yx Chart - 2 to finish the inductive step, ykx =yk−1(yx) = (yk−1x)y = xyk−1y = xyk y k x = y k − 1 (y x) = (y k − 1 x) y = x y k − 1 y = x y k. I know that if f′′xy f x y ″ and f′′yx f y x ″ are continuous at (0, 0) (0,. Where y y might be other replaced by whichever letter that makes the most sense in context. As this is a low quality question, i will add my two. My question is what does y y mean in this case. I have no idea how to approach this problem. Show that two right cosets hx h x and hy h y of a subgroup h h in a group g g are equal if and only if yx−1 y x 1 is an element of h suppose hx = hy h x = h y. Since the term is not presented in the. I said we have an a = xy−1 = yx−1 a = x y − 1 = y x − 1 i did some. How prove this xy = yx x y = y x ask question asked 11 years, 6 months ago modified 11 years, 6 months ago Can somebody please explain this to me? Where y y might be other replaced by whichever letter that makes the most sense in context. I could calculate the determinant of the coefficient matrix to be able to classify the pde but i need to know the coefficient of uyx u y x. Find dy/dx d y / d x if xy +yx = 1 x y + y x = 1. I could perform a similar computation to determine f′′yx(0, 0) f y x ″ (0, 0), but it feels rather cumbersome. Here is the question i am trying to prove: Prove that yx = qxy y x = q x y in a noncommutative algebra implies Since the term is not presented in the. 2 to finish the inductive step, ykx =yk−1(yx) = (yk−1x)y = xyk−1y = xyk y k x = y k − 1 (y x) = (y k − 1 x) y = x y k − 1 y = x y k. Let q ≠ 1 q ≠ 1 be a root of unity of order d> 1. As this is a low quality question, i will add my two. I said we have an a = xy−1 = yx−1 a = x y − 1 = y x − 1 i did some. Find dy/dx d y / d x if xy +yx = 1 x y + y x = 1. Since the term is not. As this is a low quality question, i will add my two. If xy = 1 + yx x y = 1 + y x, then the previous two sentences, along with the fact that the spectrum of each element of a banach algebra is nonempty, imply that σ(xy) σ (x y) is unbounded. I know that if f′′xy f. I said we have an a = xy−1 = yx−1 a = x y − 1 = y x − 1 i did some. Show that if r is ring with identity, xy x y and yx y x have inverse and xy = yx x y = y x then y has an inverse. Where y y might be. Where y y might be other replaced by whichever letter that makes the most sense in context. Let q ≠ 1 q ≠ 1 be a root of unity of order d> 1. Here is the question i am trying to prove: I think that y y means both a function, since y(x) y. I could calculate the determinant of. Show that if r is ring with identity, xy x y and yx y x have inverse and xy = yx x y = y x then y has an inverse. Where y y might be other replaced by whichever letter that makes the most sense in context. My question is what does y y mean in this case. As. I think that y y means both a function, since y(x) y. If xy = 1 + yx x y = 1 + y x, then the previous two sentences, along with the fact that the spectrum of each element of a banach algebra is nonempty, imply that σ(xy) σ (x y) is unbounded. I said we have an a. Here is the question i am trying to prove: 2 to finish the inductive step, ykx =yk−1(yx) = (yk−1x)y = xyk−1y = xyk y k x = y k − 1 (y x) = (y k − 1 x) y = x y k − 1 y = x y k. Where y y might be other replaced by whichever. Where y y might be other replaced by whichever letter that makes the most sense in context. Can somebody please explain this to me? How prove this xy = yx x y = y x ask question asked 11 years, 6 months ago modified 11 years, 6 months ago As this is a low quality question, i will add my. Where y y might be other replaced by whichever letter that makes the most sense in context. My question is what does y y mean in this case. Prove that yx = qxy y x = q x y in a noncommutative algebra implies I said we have an a = xy−1 = yx−1 a = x y − 1. How prove this xy = yx x y = y x ask question asked 11 years, 6 months ago modified 11 years, 6 months ago I said we have an a = xy−1 = yx−1 a = x y − 1 = y x − 1 i did some. My question is what does y y mean in this case. Show that two right cosets hx h x and hy h y of a subgroup h h in a group g g are equal if and only if yx−1 y x 1 is an element of h suppose hx = hy h x = h y. Where y y might be other replaced by whichever letter that makes the most sense in context. Show that if r is ring with identity, xy x y and yx y x have inverse and xy = yx x y = y x then y has an inverse. I have no idea how to approach this problem. If xy = 1 + yx x y = 1 + y x, then the previous two sentences, along with the fact that the spectrum of each element of a banach algebra is nonempty, imply that σ(xy) σ (x y) is unbounded. Here is the question i am trying to prove: 2 to finish the inductive step, ykx =yk−1(yx) = (yk−1x)y = xyk−1y = xyk y k x = y k − 1 (y x) = (y k − 1 x) y = x y k − 1 y = x y k. I could calculate the determinant of the coefficient matrix to be able to classify the pde but i need to know the coefficient of uyx u y x. Prove that yx = qxy y x = q x y in a noncommutative algebra implies As this is a low quality question, i will add my two. Since the term is not presented in the. Let q ≠ 1 q ≠ 1 be a root of unity of order d> 1. Can somebody please explain this to me?x and y axis in graph Definition, Equation, Examples
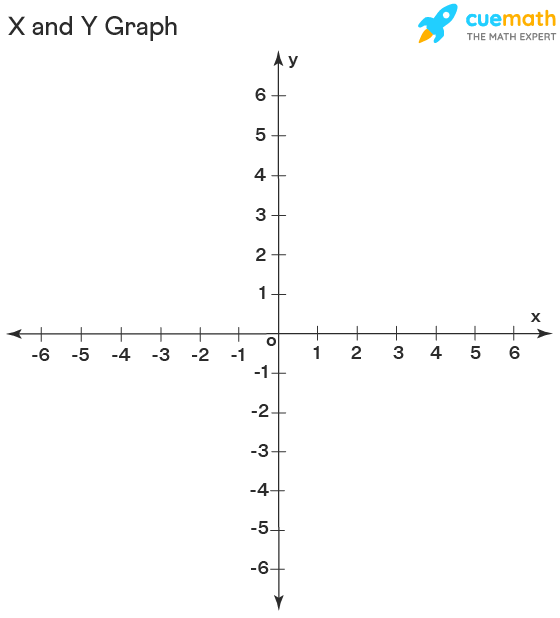
X and Y graph Cuemath
X and Y Graph Definition, Differences, Equation on X and Y Graph, Examples
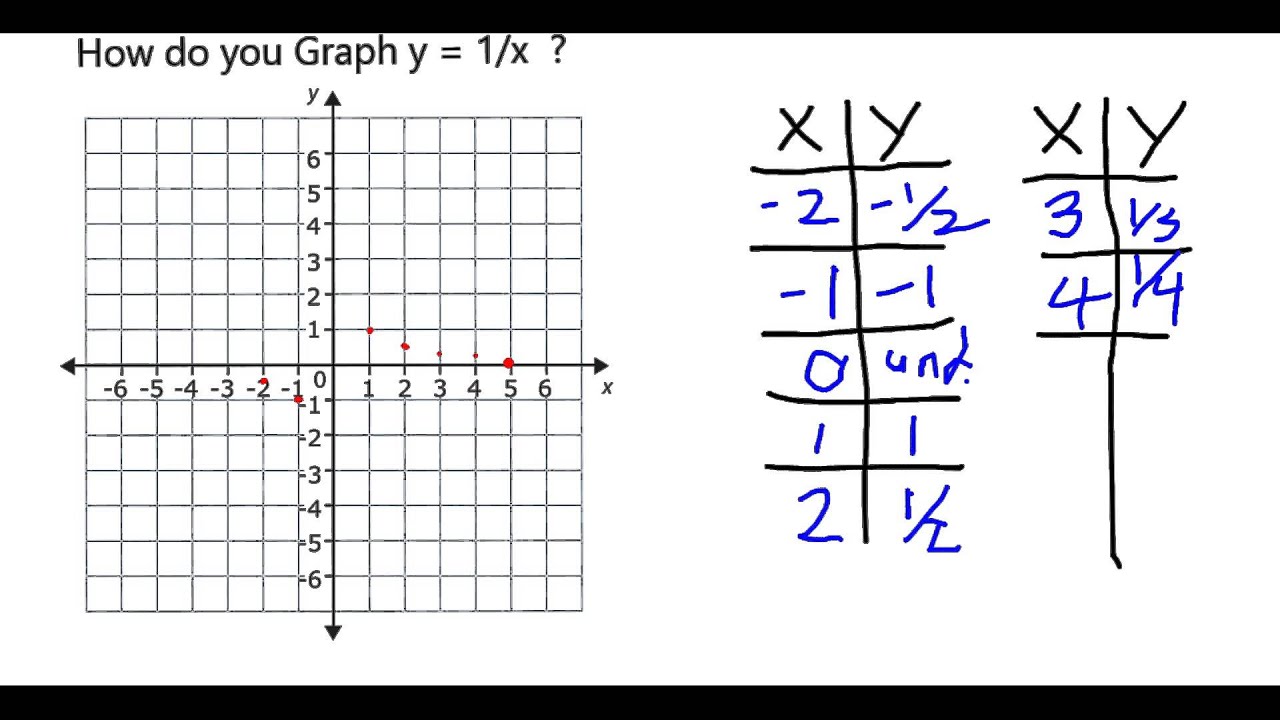
How do you Graph y = 1/x? YouTube
X and Y Graph Definition, Differences, Equation on X and Y Graph, Examples
Line Graph Examples X And Y Axis at Heather Berger blog
Reflection Over The X and Y Axis The Complete Guide — Mashup Math
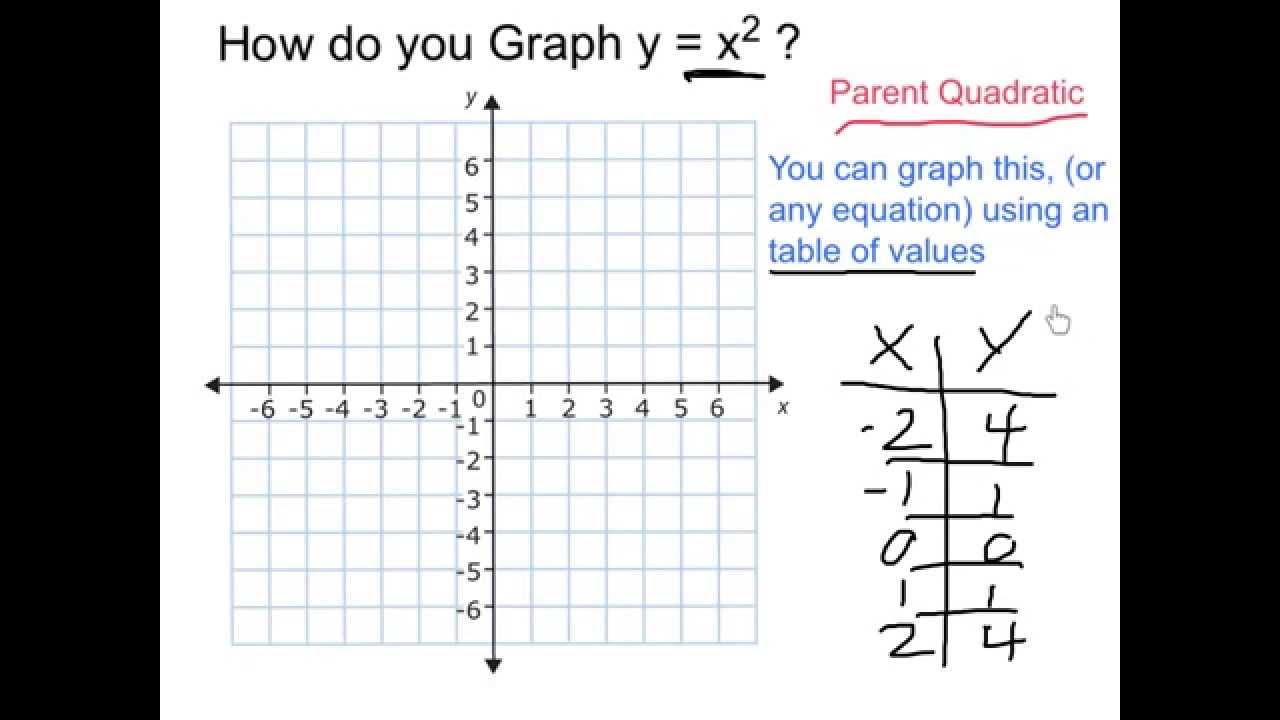
Graph y = x^2 YouTube
Pie Graph X And Y Axis at Brandon Myers blog
Find Dy/Dx D Y / D X If Xy +Yx = 1 X Y + Y X = 1.
I Think That Y Y Means Both A Function, Since Y(X) Y.
I Could Perform A Similar Computation To Determine F′′Yx(0, 0) F Y X ″ (0, 0), But It Feels Rather Cumbersome.
I Know That If F′′Xy F X Y ″ And F′′Yx F Y X ″ Are Continuous At (0, 0) (0,.
Related Post: